最小二乘法

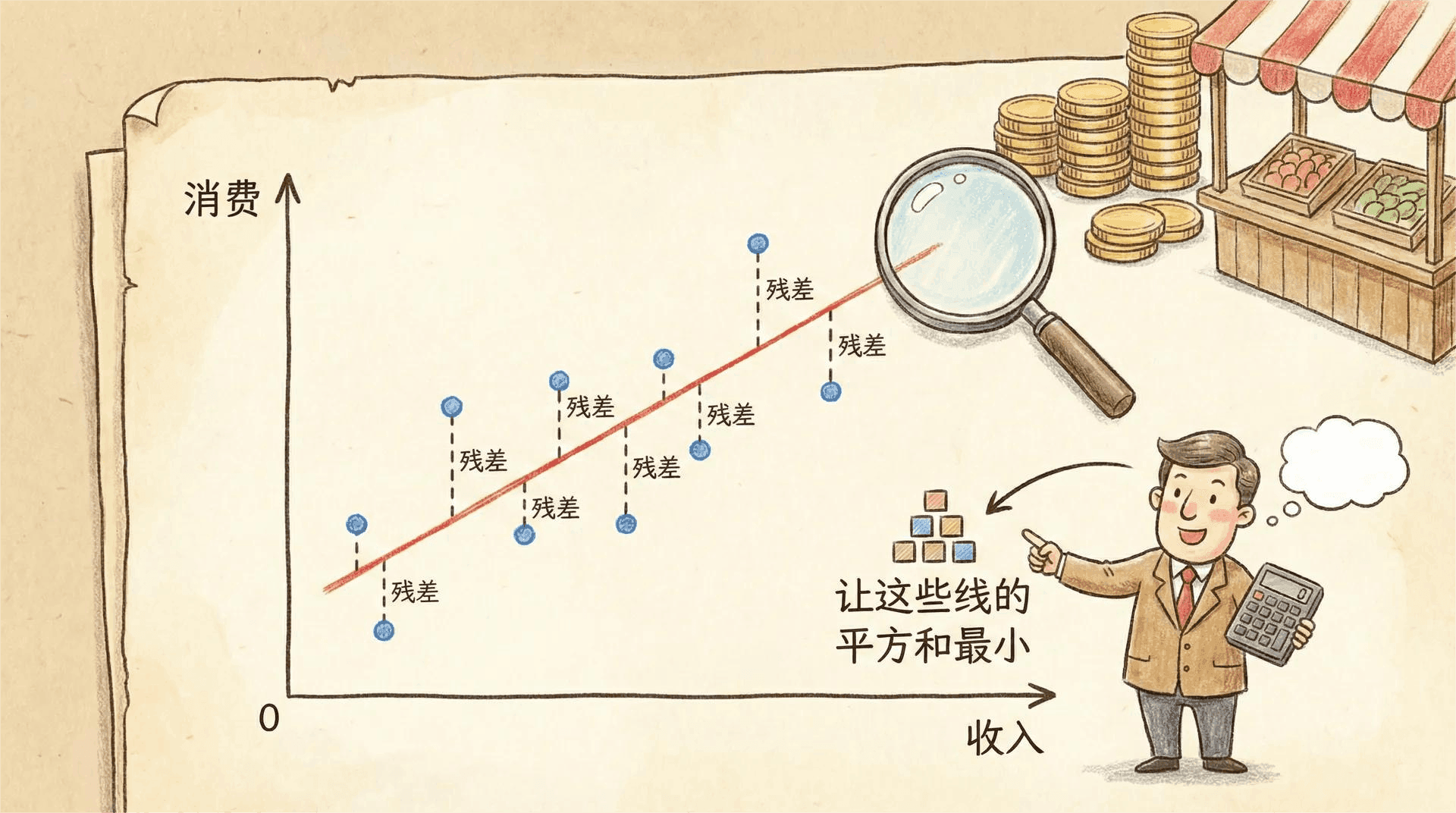
在经济学研究中，我们经常需要从一组看似无序、杂乱的数据点中寻找背后的模式与规律。例如，你是一位房地产分析师，手中掌握着北京市100套房子的面积和价格数据。这些数据在平面坐标图中分布得零零散散，表面上看不到明显的关联，但你的直觉告诉你，房屋面积和价格之间应当存在某种关系。你的任务就是要用科学的方法，从这些“噪声”中提取出有用的信号。

这时，最小二乘法就派上了用场。可以把它想象成一位经验丰富的裁缝，能够在无数数据点中为你量身裁剪出一条“最合身”的直线。这条直线不仅仅是对所有数据的简单连接，而是以特定原则（使预测值与实际值的偏差平方和最小）来反映变量之间最根本的关系。

在前面的内容中，我们已经建立了基本的线性回归模型框架。现在，我们面临的核心实际问题是：如何通过已有数据，合理估计模型中的未知参数。虽然现实中存在多种估计方法可供选择，但最小二乘法因其直观、便于计算，同时具备坚实的理论基础，因此成为众多学科中最主流、最受欢迎的方法。即便在个别情况下有其他更优的估计方法，最小二乘法依然是重要的参考基准。实际上，许多新发展起来的改进方法，本质上都是对最小二乘法的某种扩展或修正。

总而言之，最小二乘法既是实用的数据工具，也是理解经济学实证分析的基础。

---

最小二乘回归的基本思想

在经济学和数据分析中，我们常用如下随机关系式来描述变量之间的关系：

$$y_i = x_i\beta + \varepsilon_i$$

在理解和使用这个公式时，有几个重要概念要注意区分：

例如，若我们正在研究中国消费者的收入与支出关系，真实的总体关系是

$$E[\text{支出} \mid \text{收入}] = x_i\beta$$

但在现实研究中，我们只能基于样本数据，得到类似

$$\hat{y}_i = x_ib$$

的估计关系。这里的 $x_i$ 代表每个样本点的自变量，$\hat{y}_i$ 是模型的预测值。

残差的几何意义

对于任意估计值 $b$，我们定义第 $i$ 个观测的残差为：

$$e_i = y_i - x_ib$$

残差 $e_i$ 反映了实际观测值与预测值之间的“距离”。以房价预测为例，若实际价格为500万元，而模型预测为480万元，则残差为20万元。更小的残差意味着模型预测得越精确。几何上，每个残差可以看作数据点到拟合直线的垂直距离。

---

最小二乘系数向量的推导

优化目标的设定

最小二乘法的核心思想是：从所有可能的直线（或超平面）中，选出那条使所有数据点到直线的“垂直距离”平方和最小。用数学语言表达为：

$$S(b) = \sum_{i=1}^n (y_i - x_ib)^2$$

这个目标实际上是在“拟合”中追求整体误差总量的最小化，也即将预测误差的平方和降到最低。

为何选择平方和而不是绝对值和？

• 平方和在数学上具有良好性质，便于求导和后续理论推导。
• 对异常值敏感，有助于模型在一般样本下表现最优（但在异常值多的情况要注意）。
• 有明确的统计解释，奠定了高斯-马尔可夫定理等重要结论的基础。

矩阵形式的表达

对于多元回归模型，我们常用矩阵表达，大大简化推导和计算：

$$S(b) = (y - Xb)^\mathrm{T}(y - Xb)$$

其中 $y$ 是 $n \times 1$ 的观测向量，$X$ 是 $n \times k$ 的自变量矩阵，$b$ 是 $k \times 1$ 的回归系数向量。

将 $S(b)$ 展开可得：

$$S(b) = y^\mathrm{T}y - 2y^\mathrm{T}Xb + b^\mathrm{T}X^\mathrm{T}Xb$$

求解过程

要找到最小值点，需要对 $b$ 求偏导并令其等于0，得到一阶最优条件：

$$\frac{\partial S(b)}{\partial b} = -2X^\mathrm{T}y + 2X^\mathrm{T}Xb = 0$$

这就得到了著名的正规方程组（Normal Equations）：

$$X^\mathrm{T}Xb = X^\mathrm{T}y$$

若 $X^\mathrm{T}X$ 可逆（即$X$列满秩），解为：

$$\mathbf{b^*} = (X^\mathrm{T}X)^{-1}X^\mathrm{T}y$$

这个公式是最小二乘法的核心结果，$\mathbf{b^*} = (X^\mathrm{T}X)^{-1}X^\mathrm{T}y$ 告诉我们如何利用样本数据直接计算最优的回归系数估计值。

二阶条件验证

为了验证确实得到的是最小值而不是最大值或鞍点，我们考察二阶导数矩阵（Hessian）：

$$\frac{\partial^2 S(b)}{\partial b \partial b^\mathrm{T}} = 2X^\mathrm{T}X$$

只要 $X^\mathrm{T}X$ 是正定矩阵（通常这要求 $X$ 满列秩，回归变量之间无完全多重共线性），最优解 $b$ 就是使误差平方和最小的唯一解。因此，这种几何和代数上的最优性为最小二乘法打下了坚实基础。

补充说明：这种推导方式不仅适用于一元线性回归，也同样适用于含有多个变量的多元线性回归，为实际操作与理论分析提供了完整的数学依据。

投资方程案例

为了更深入理解最小二乘法的实际应用，我们借助一个具体的宏观经济案例展开。假设我们希望研究中国实际投资($Y$)与一系列经济因素之间的关系，包括：实际GDP($G$)、时间趋势($T$)、利率($R$)、以及通胀率($P$)。

这些变量的含义和单位如下所示：

为了便于演算，我们先考虑一个简化模型，只包含三个自变量（常数项、时间趋势和实际GDP）：

$$Y_i = b_1 + b_2 T_i + b_3 G_i + \varepsilon_i$$

其中 $i=1,2,\ldots,n$。

三变量回归——手工推导正规方程

根据最小二乘法的原理，我们要最小化残差平方和：

$$S(b_1, b_2, b_3) = \sum_{i=1}^n \left( Y_i - b_1 - b_2 T_i - b_3 G_i \right)^2$$

对各个回归系数分别求偏导并令其为零，得到一阶条件，推导出下列正规方程组：

$$\begin{cases} b_1 n + b_2 \sum_{i=1}^n T_i + b_3 \sum_{i=1}^n G_i = \sum_{i=1}^n Y_i \\ b_1 \sum_{i=1}^n T_i + b_2 \sum_{i=1}^n T_i^2 + b_3 \sum_{i=1}^n T_i G_i = \sum_{i=1}^n T_i Y_i \\ b_1 \sum_{i=1}^n G_i + b_2 \sum_{i=1}^n T_i G_i + b_3 \sum_{i=1}^n G_i^2 = \sum_{i=1}^n G_i Y_i \end{cases}$$

或者更紧凑地写为矩阵形式：

$$\begin{pmatrix} n & \sum T_i & \sum G_i \\ \sum T_i & \sum T_i^2 & \sum T_i G_i \\ \sum G_i & \sum T_i G_i & \sum G_i^2 \end{pmatrix} \begin{pmatrix} b_1 \\ b_2 \\ b_3 \end{pmatrix} = \begin{pmatrix} \sum Y_i \\ \sum T_i Y_i \\ \sum G_i Y_i \end{pmatrix}$$

手动计算这组三元一次方程组是非常繁琐的。对于更高维度的多元回归，这种计算几乎不可能手工完成。

现代经济学与计量分析中，我们通常依赖如 R、Python、Stata 等统计软件，通过内置的线性回归函数，直接调用最小二乘公式

$$\mathbf{b^*} = (X^\mathrm{T}X)^{-1} X^\mathrm{T} y$$

高效、准确地求出回归系数。但理解上述推导和正规方程结构，对于解释回归结果背后的经济含义、检查模型设定、检测异常及错误，仍然非常关键。

因此，学习最小二乘法不仅是理解统计计算，更是深入体会“由数据支撑的经济学解释”。

---

最小二乘解的重要性质

残差的三个基本特性

当我们运用最小二乘法拟合数据集后，所得的残差 $e_i$ 具有以下三个极其重要的基本性质，理解这些性质对于深入分析经济数据、判断模型有效性有着举足轻重的意义。

特性一：残差之和为零

在包含常数项的回归模型中，所有残差之和恒为零，即

$$\sum_{i=1}^n e_i = 0$$

这一点意味着什么？可以理解为：如果你的回归模型合理、无偏，那么高估和低估将会在总体上相互抵消，模型的预测结果在全局上是“平衡”的。例如，根据这个性质，预测房价时偶尔低估或高估并不可怕，关键是不能长期、系统性地偏高或偏低。

特性二：回归超平面必然通过均值点

多元线性回归中的回归超平面（或在两变量情况下为回归直线）必然通过所有变量的均值点，即

$$\bar{y} = \bar{\mathbf{x}}^\mathrm{T}\mathbf{b}$$

其中 $\bar{y}$ 是因变量的均值，$\bar{\mathbf{x}}$ 是解释变量的均值向量，$\mathbf{b}$ 是估计系数向量。这一性质说明，不论数据如何分布，回归模型的拟合总是会“穿过”样本均值点。例如，若平均收入为 $5$ 万元，平均消费为 $3$ 万元，则拟合的消费函数一定经过点 $(5, 3)$。

特性三：拟合值的均值等于实际值的均值

最小二乘回归保证拟合值的均值与因变量的实际均值相等，即

$$\frac{1}{n}\sum_{i=1}^n \hat{y}_i = \frac{1}{n}\sum_{i=1}^n y_i$$

这确保了模型的预测在样本总体上不会存在系统性高估或低估，使得回归在统计意义上“对准”总体。

投影的几何解释

最小二乘法的本质可以用线性代数中的“投影”思想来直观解释。其核心思想是：将观测向量 $\mathbf{y}$ 投影到由解释变量矩阵 $\mathbf{X}$ 张成的列空间上。

投影矩阵与残差制造矩阵

我们可以定义两个在回归分析中极为重要的矩阵：

• 投影矩阵： $$\mathbf{P} = \mathbf{X}(\mathbf{X}^\mathrm{T}\mathbf{X})^{-1}\mathbf{X}^\mathrm{T}$$
• 残差制造矩阵： $$\mathbf{M} = \mathbf{I} - \mathbf{P}$$

这两个矩阵具有如下的性质：

• 对称性（Symmetry）：$\mathbf{P}^\mathrm{T} = \mathbf{P}, \;\; \mathbf{M}^\mathrm{T} = \mathbf{M}$
• 幂等性（Idempotent）：$\mathbf{P}^2 = \mathbf{P},\;\; \mathbf{M}^2 = \mathbf{M}$
• 正交性（Orthogonality）：$\mathbf{P}\mathbf{M} = \mathbf{0},\;\; \mathbf{M}\mathbf{P} = \mathbf{0}$

这些性质对后续的统计推断、方差分解等有很大帮助。

几何直观展示

在上述几何框架中：

• 灰色封闭区域代表解释变量 $\mathbf{X}$ 张成的列空间
• 蓝色实线代表观测向量 $\mathbf{y}$ 在该子空间内的正交投影，即拟合值 $\hat{\mathbf{y}} = \mathbf{P}\mathbf{y}$
• 红色虚线则为残差向量 $\mathbf{e} = \mathbf{y} - \hat{\mathbf{y}}$，它与列空间正交

平方和的分解

最小二乘法自然带来了经典的平方和三分法，即，一个观测向量可分解为回归部分与残差部分，两者平方和等于总平方和。具体公式为：

$$\mathbf{y}^\mathrm{T}\mathbf{y} = \hat{\mathbf{y}}^\mathrm{T}\hat{\mathbf{y}} + \mathbf{e}^\mathrm{T}\mathbf{e}$$

其中

• $\mathbf{y}^\mathrm{T}\mathbf{y}$ 称为“总平方和”（Total Sum of Squares, TSS）
• $\hat{\mathbf{y}}^\mathrm{T}\hat{\mathbf{y}}$ 称为“回归平方和”（Regression Sum of Squares, RSS）
• $\mathbf{e}^\mathrm{T}\mathbf{e}$ 称为“残差平方和”（Residual Sum of Squares, ESS）

这正是欧氏空间中的毕达哥拉斯定理的统计实现——回归分解为正交分量，解释了为什么能用 $R^2$ 来评价模型拟合优度：

$$R^2 = 1 - \frac{\mathbf{e}^\mathrm{T}\mathbf{e}}{\mathbf{y}^\mathrm{T}\mathbf{y}}$$

---

分割回归与偏回归

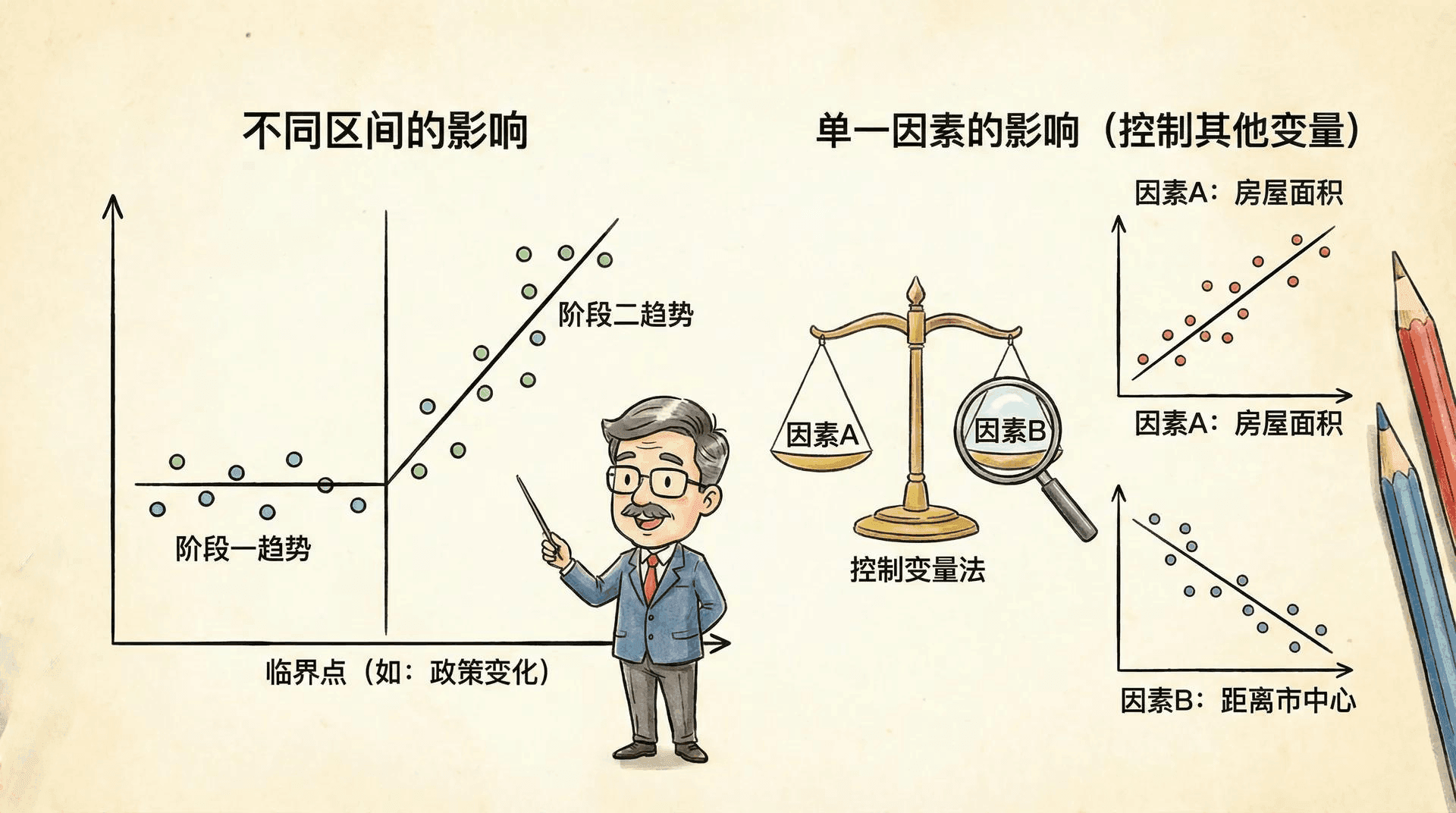
在实际经济分析和建模过程中，我们时常要面对这样的问题：在一个多元回归模型中，如何仅研究某个解释变量对因变量的“净效应”？这就需要用到分割回归和偏回归的理论。

问题的提出

假设我们想研究教育年限对收入的影响，但又要控制住年龄这一干扰因素。模型结构如下：

$$\text{收入} = \beta_1 + \beta_2 \times \text{教育年限} + \beta_3 \times \text{年龄} + \varepsilon$$

如果只关心 $\beta_2$，是否一定要整体估计所有参数？答案是否定的。我们可以利用分割回归理论，只专注于我们关心的变量。

正交回归定理

基本结论：如果两个解释变量 $X_1$ 和 $X_2$ 满足正交，即

$$X_1^\mathrm{T} X_2 = 0$$

那么对 $y$ 进行多元回归与分别对 $X_1$、$X_2$ 做简单回归，二者所得到的回归系数完全一致。

经济直觉：当解释变量互不相关时，某个变量对因变量的边际效应不会受到其他变量影响，和一元回归一致。

Frisch-Waugh-Lovell（FWL）定理

这是回归理论最核心的定理之一，为我们“分离”出变量的净效应提供了理论与操作基础。

定理内容： 在 $y$ 关于 $X_1$ 和 $X_2$ 的多元回归中，$X_2$ 的系数可通过以下两步获得：

1. 将 $y$ 对 $X_1$ 回归，取残差（记为 $y^*$）；将 $X_2$ 对 $X_1$ 回归，也取残差（记为 $X_2^*$）
2. 用 $y^*$ 对 $X_2^*$ 做简单回归，得到的系数就是原多元回归中 $X_2$ 的回归系数。

公式化表述为：

$$\text{步骤一：}\quad y^* = \mathbf{M}_1 y, \quad X_2^* = \mathbf{M}_1 X_2$$ $$\text{步骤二：}\quad\quad y^* = \gamma X_2^* + \text{误差} \Rightarrow \gamma = \beta_2$$

教育收益率

以中国数据实际分析为例：

均值偏差（中心化）形式的回归

FWL定理在包含常数项时有一个极为简洁漂亮的推论：

推论： 在有常数项的多元回归中，斜率系数等价于用均值偏差数据（所有变量减去各自均值）作无常数回归所获得的系数。

即，将数据中心化后（减去均值）进行回归，所得的 $\mathbf{b}$ 与原始模型中的斜率完全一致。

步骤如下：

这一结论进一步强调了回归系数所刻画的是“其他条件保持不变”时某一解释变量的边际效应，是理解经济变量之间“净关系”的理论基础。

---

偏回归系数与偏相关系数

偏回归系数的经济含义

在多元回归模型中，一个核心问题是：“当控制了其他条件时，某个解释变量对因变量的真实影响有多大？” 这实际上是在问：“ceteris paribus（其他条件不变）下，变量$z$的边际效应是多少？” 这正是偏回归系数（Partial Regression Coefficient）所要回答的问题。

偏回归系数反映了当其他所有变量保持恒定时，某一个解释变量的变化会引起因变量的变化幅度。以回归模型

$$y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \cdots + \beta_K x_K + \varepsilon$$

为例，$\beta_j$就是$x_j$对$y$的偏回归系数，表示在控制了其余$x$之后，$x_j$每变动一个单位，$y$的期望变动$\beta_j$个单位。

经济学中著名的“ceteris paribus”分析就是用偏回归思想：比如在研究教育对收入的影响时，我们希望控制年龄、性别、地区等其他因素，只看教育这一个因素的“净贡献”——即$\beta_{\text{教育}}$。

偏相关系数的计算方法与理解

偏相关系数（Partial Correlation Coefficient） 衡量的是“在控制了其他变量影响之后，两个变量之间还剩下多少相关性”，即去除了其他因素“净化”出来后的线性相关程度。

假设我们关注$y$与$z$的关系，并希望“控制”住变量$X$（可能是一组变量），则具体计算步骤如下：

也可以用公式写为：

$$r_{yz\cdot X} = \frac{\operatorname{Cov}(y^\ast, z^\ast)}{\sigma_{y^\ast} \sigma_{z^\ast}}$$

这里$y^\ast$与$z^\ast$就是剔除了控制变量后的“净量”，求它们的相关性即可。

这种方法可以广泛推广到多个变量的控制、甚至分层分析，是理解“真实相关性”与“表面相关性”区别的基础工具。

偏相关系数、$t$统计量与$R^2$的关系

在多元回归分析中，偏相关系数与$t$统计量之间有着直接联系，公式表达如下：

$$r^2_{y z \cdot X} = \frac{t_z^2}{t_z^2 + \text{df}}$$

其中：

• $r^2_{y z \cdot X}$：在控制$X$之后，$y$和$z$的偏相关系数的平方；
• $t_z$：多元回归中$z$对应的$t$统计量；
• $\text{df}$：自由度，通常为$n-K-1$，$K$为解释变量的个数，$n$为样本容量。

由此可以倒推，如果知道$t$统计量和自由度，即可便捷算出$y$和$z$在给定其他变量后的相关性大小。这一公式连接了显著性检验与相关性分析，具有重要应用价值。

投资方程的相关性

下面我们用一个实际的回归例子来体会“简单相关系数”与“偏相关系数”的区别，以及为什么偏回归和多元回归极其重要：

这种现象是多数实际经济、社会、医学等数据分析场景中的常态：表面关系与净关系可能完全相反，不做“净化”分析，结论极易误导。

---

拟合优度与方差分析

R²的基本定义与公式

拟合优度（Goodness-of-fit）衡量回归模型对观测数据变异的解释能力。最常用的指标是决定系数$R^2$（R-squared），给我们这样一个直观问题的答案：“模型解释了因变量总变异的百分之多少？”

标准$R^2$公式为：

$$R^2 = \frac{\text{回归平方和}}{\text{总平方和}} = \frac{SSR}{SST} = 1 - \frac{SSE}{SST}$$

它们定义如下：

• 总平方和（全变异）：$SST = \sum_{i=1}^n (y_i - \bar{y})^2$
• 回归平方和（模型解释变异）：$SSR = \sum_{i=1}^n (\hat{y}_i - \bar{y})^2$
• 残差平方和（误差）：$SSE = \sum_{i=1}^n (y_i - \hat{y}_i)^2$

所以$R^2$取值$[0,1]$，数值越大表示模型解释能力越强。

R²的直观解释

假设我们分析中国各省$GDP$差异成因：

若$R^2 = 0.75$，代表：

• 模型解释了$75\%$的$GDP$差异（归因于回归方程中的解释变量）
• 还有$25\%$差异无法解释（残差、噪音或遗漏变量影响）
• 通常认为$0.75$是一个很高的拟合优度

方差分析表（ANOVA Table）

标准回归模型常配合方差分析表总结各项变异分布：

$MSR$常用于构造$F$检验，检验模型整体显著性。

为什么要引入调整$R^2$

普通$R^2$有个“软肋”：加变量$R^2$永不下降，哪怕新变量毫无用处！这如同学生盲目扩充复习科目，最终拖后腿。

所以引入“调整$R^2$”$\bar{R}^2$（Adjusted$R^2$），弥补$R^2$惩罚复杂性不足。其定义为：

$$\bar{R}^2 = 1 - \frac{\frac{SSE}{n-K}}{\frac{SST}{n-1}}$$

调整后的特点：

• 无关变量会降低$\bar{R}^2$
• $\bar{R}^2$不一定比$R^2$大，有时可能为负，提醒模型几乎不能拟合数据
• 在模型比较与特征选择等任务中，$\bar{R}^2$价值更高

$R^2$的常见误区与陷阱

陷阱一：不同数据类型$R^2$不可简单比较

如时间序列数据$R^2$通常远高于截面数据，这不是模型更好，只是反映数据自相关性。不要简单迷信“高$R^2$”。

陷阱二：不同类型回归$R^2$不可比

如线性模型$y = \beta_0 + \beta_1 x + \varepsilon$与对数线性$\ln y = \beta_0 + \beta_1 x + \varepsilon$，不可直接比$R^2$，因因变量本身已变。

陷阱三：没有常数项的模型$R^2$偏大或异常

模型若不包含截距项（常数），$R^2$的计算原理就会失效，甚至可能$>1$或为负，则不能正常使用，应警惕数据和模型结构是否设计合理。

不同应用下$R^2$的典型范围与意义

不同领域、不同数据结构$R^2$的合理区间差异极大：

$R^2$只是评估的一个维度。有时即便$R^2$较低，只要每个系数都有明确的经济意义与统计显著性，这个模型依然很有价值。反之，$R^2$极高但系数荒谬、难以解释时，模型其实毫无实际用处。

---

线性变换回归

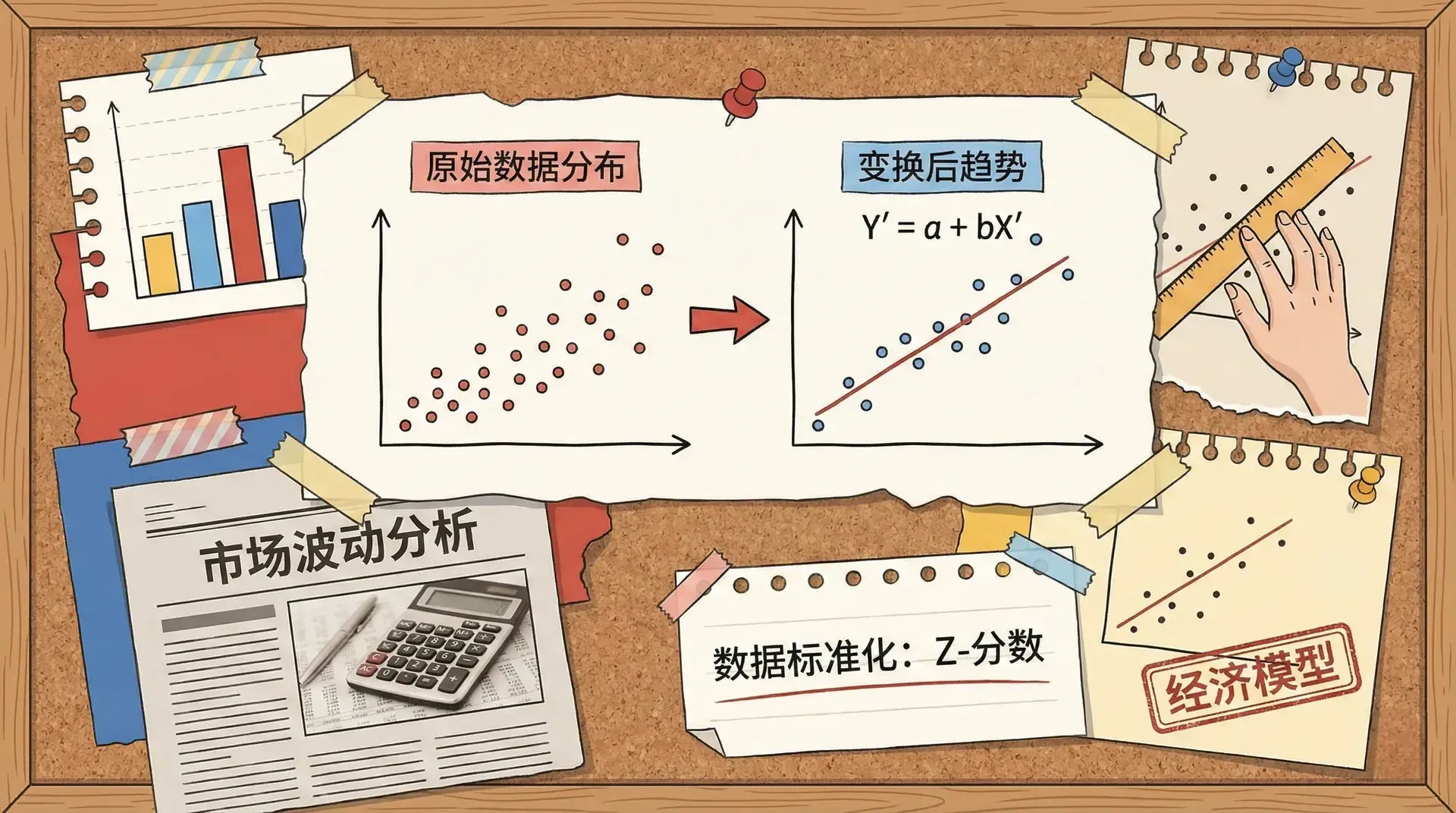
为什么要做变量变换？

在实际经济分析与回归建模过程中，经常需要对变量进行线性变换。这些变换主要出于以下几类动因：

• 单位转换：比如将 GDP 从“亿元”转换为“万亿元”，或者将时长从“小时”换算为“分钟”，仅仅是刻度变化，变量本身的含义不变。
• 理论需要：有些经济理论要求我们用衍生变量，例如根据“宽度”“高度”得到“面积”与“长宽比”等组合特征。此时新变量为原变量的线性组合。
• 数据处理：常见如对变量做标准化（z-score），消除单位差异，使结果可比。

变量变换不仅仅是代数技巧，也关乎经济解释和理论本质。下面我们以艺术品价格案例说明其内在联系。

艺术品拍卖定价

如果我们希望用回归模型分析莫奈画作的拍卖价格。存在两套理论思路：

理论一：尺寸主导假设

$$\ln(\mathrm{价格}) = \beta_1 + \beta_2\ln(\mathrm{宽度}) + \beta_3\ln(\mathrm{高度}) + \varepsilon$$

理论二：面积与比例论

$$\ln(\mathrm{价格}) = \gamma_1 + \gamma_2\ln(\mathrm{面积}) + \gamma_3\ln(\mathrm{长宽比}) + u$$

其中：

• 面积：$\mathrm{面积} = \mathrm{宽度} \times \mathrm{高度}$
• 长宽比：$\mathrm{长宽比} = \mathrm{宽度} / \mathrm{高度}$

注意到：

$$\ln(\mathrm{面积}) = \ln(\mathrm{宽度}) + \ln(\mathrm{高度}), \qquad \ln(\mathrm{长宽比}) = \ln(\mathrm{宽度}) - \ln(\mathrm{高度})$$

所以这两组解释变量本质上是原变量的线性变换。

变量线性变换的矩阵表示

我们可以将上述两个理论之间的“变量变换”写成矩阵形式。设

$$Z = \begin{bmatrix} z_1 \\ z_2 \\ z_3 \end{bmatrix} = P \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} = PX$$

其中：

• $x_1$：常数项，$x_2$：$\ln(\mathrm{宽度})$，$x_3$：$\ln(\mathrm{高度})$
• $z_1 = x_1$，$z_2 = x_2 + x_3$，$z_3 = x_2 - x_3$

变换矩阵为

$$P = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 1 \\ 0 & 1 & -1 \end{bmatrix}$$

用表格再梳理：

线性变换回归定理

定理：
假设有原始回归

$$y = X\beta + \varepsilon$$

以及变换变量回归

$$y = Z\gamma + u, \quad \text{其中}\ Z = XP$$

且 $P$ 为非奇异（即可逆）矩阵。则有：

1. 回归系数变换关系 $$\gamma = P^{-1}\beta$$
2. 两模型的$R^2$完全一致 $$R^2_{X} = R^2_{Z}$$
3. 残差向量完全一致 $$\hat{\varepsilon} = \hat{u}$$

也就是说，任何线性可逆的变量变换不会改变拟合优度和残差，只会线性变换系数解释本身。

线性变换定理的实际应用

该定理赋予回归分析巨大的灵活性，带来诸多实际好处：

应用一：单位变换与系数缩放

若某解释变量 $x_2$ 由“万元”改为“元”，则其数值变为原来的 $10,000$ 倍。此时，无需重新回归，只要把对应回归系数$\beta_2$除以$10,000$即可：

$$\begin{align*} \text{原模型：}\,\ & y = 3\, \text{(万元)} \times x_2 + \ldots \\ \text{变换后：}\,\ & y = 0.0003\, \text{(元)} \times x_2 + \ldots \end{align*}$$

应用二：理论模型等价性检验

对于上述莫奈画作的两种理论，两套解释变量通过$P$线性变换可互相推出。这意味着它们对数据的解释力完全等价，只是经济解释侧重点不同。

应用三：标准化回归的便利

分析多元数据时，变量的尺度不同，标准化即对每个变量减去均值再除以标准差

$$z_i = \frac{x_i - \overline{x}_i}{\mathrm{std}(x_i)}$$

标准化回归恰好是对原回归变量做线性变换。利用线性变换定理，标准化模型的系数可以直接由原始模型系数与标准差计算得出，而$R^2$不变，残差分布也一致。因此变量标准化便于比较不同自变量的重要性，而不会影响整体拟合优度。

---

要点总结

核心概念回顾

经济学直觉

最小二乘法不仅是数学分析的工具，更深刻地体现了经济学中的核心思维。首先，最小二乘法中的偏回归系数揭示了“边际分析”的思想——每一个系数都在度量单个解释变量对因变量的边际影响，这与经济学对边际效应的重视不谋而合。同时，最小二乘解也是“均衡思想”的具体体现：通过最小化残差平方和，模型在所有可能的解中达到了一种“总成本”最小的均衡状态。在诸多无偏估计量中，最小二乘估计量的“效率”也是最高的，它拥有最小的方差。此外，最小二乘法还是一种强有力的信息提取手段，能够从噪音和扰动中提炼出数据背后的真实信号。