连接能量与熵
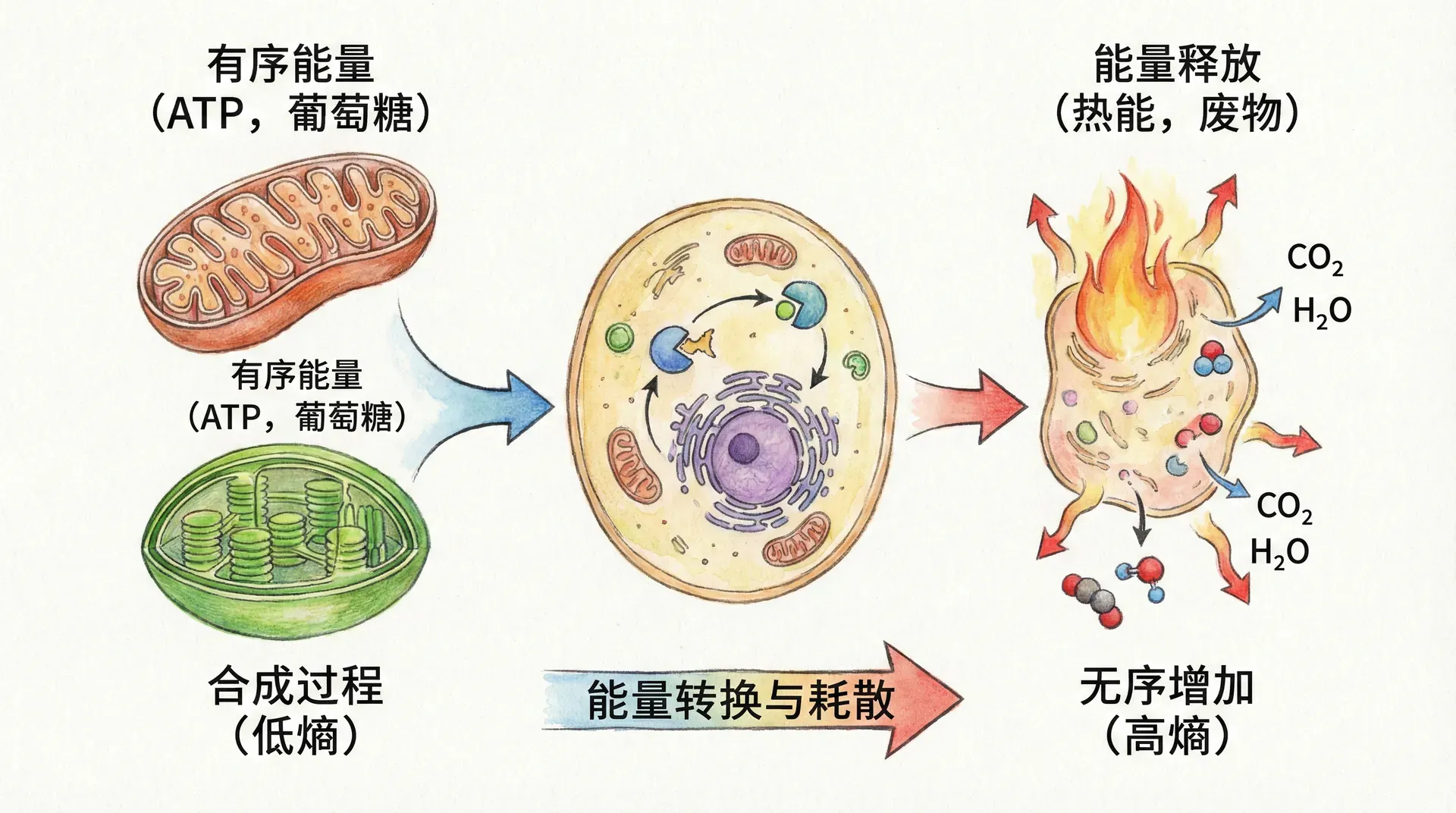
在北京的冬天和夏天,我们会发现一个有趣的现象:冬季的街道上行人稀少,大多数人聚集在温暖的室内;而夏季的公园里,人们则更愿意在阴凉处休息,避开正午炎热的阳光。这个看似简单、与日常紧密相关的生活现象,其实反映了一个深刻的科学原理——能量分布规律。为什么人们喜欢在舒适的环境中停留?归根结底,是能量(或热量)交换和分布的结果。在生物学的微观世界中,数量庞大的分子同样会“选择”它们更容易停留的位置,这正如我们今天要学习的玻尔兹曼分布所描述的那样。
玻尔兹曼分布是连接宏观热力学与微观分子行为的重要桥梁,它不仅帮助我们理解为什么生物系统能够在复杂的环境中保持稳定、为什么酶反应具有特定的温度依赖性,还能解释蛋白质折叠过程所遵循的能量规律。更进一步,当我们探索生命现象的本质时,会发现玻尔兹曼分布的思想贯穿于能量分配、物质代谢、细胞活动等一系列生命活动之中。无论是在寒冷冬夜里的人体维持体温,还是在热带雨林里植物的蒸腾作用,背后都有能量和熵的共同作用。
能量分布与系统多重度
分子的“居住选择”
我们可以把分子的能级分布想象成一栋有好多层楼的公寓大楼。每一层楼代表一个不同的能量水平。住在低层的居民(低能态分子)上下楼梯需要消耗的体力较少,而住在高层的居民(高能态分子)则需要花费更多的体力。在没有电梯的情况下,绝大多数居民自然会选择住在较低的楼层,因为这样更容易、能耗也低,只有少数体力充沛的人会选择高楼层。
这个生活化的比喻直观地说明了分子在不同能级上的分布规律:在生物系统中,分子总体倾向于占据能量较低的状态,因为这样“更省力”,但由于环境温度的存在,总会有一部分分子获得了足够的能量因而跃迁到较高的能级。这个现象其实很普遍,例如细胞内的能量分子(如ATP)在高能状态下的数量很少,而低能态(如ADP和Pi)的数量较多。打个比方,就像商场里打折时,大多数人都会聚集在低价商品区域,而高价区则少有人问津,但始终会有人为了心仪的商品愿意“花大价钱”。
多重度的概念
多重度是指系统在特定总能量下可能存在的不同微观状态数目。就像同一栋楼的同一层可能有多套房间一样,同一个能级也可能对应多种不同的分子排列方式。
在生物学中,多重度的概念对于理解蛋白质折叠等复杂过程非常关键。假如蛋白质分子在自我折叠的过程中,可能存在数万甚至上亿种不同的空间构象,每一种构象都对应一个特定的能量值。正确折叠的蛋白质通常处于能量最低的状态,这个状态的多重度也许不大(就像一楼只有几间房),而错误折叠的状态虽然能量较高,但对应的构象组合却极其丰富(就好比高层楼房间很多)。这解释了为何在没有分子伴侣的帮助下,蛋白质偶尔会误折叠,也暗示了多重度在调节生物分子功能中的重要作用。
此外,多重度与熵概念息息相关。熵本质上就是系统的多重度的对数度量,反映了系统的无序度和可能的微观排列方式数量。对于生物体而言,能量和多重度的相互作用决定了生命活动的方向——系统趋向于多重度(即熵)最大的状态,由此实现能量的最优分配。
中国传统中医的能量观
中国传统中医中的“气”的概念,虽然在现代分子生物学框架下需要新的解释,但其背后对能量流动和平衡的关注,其实与现代统计力学尤其是玻尔兹曼分布的理念有着有趣的相通之处。中医认为,人体的“气”在经络与脏腑之间流动,调节着生命活动的动态平衡;而统计力学认为,分子能量的分布倾向于实现系统整体的熵最大化和平衡状态。事实上,你可以把“气”的流动看作能量在复杂系统内部不断重新分配和调整的过程。生病时,“气机阻滞”,可能类比为能量分布异常或熵减少,健康状态则对应系统处于较高多重度、能量分布更均匀平衡的状态。
这种整体性的能量分布思想为我们提供了跨文化的理论视角。正如中医讲究“阴阳平衡”,玻尔兹曼分布也告诉我们,所有系统都倾向于达到平衡态,并在此过程中衍生出复杂的生命现象。
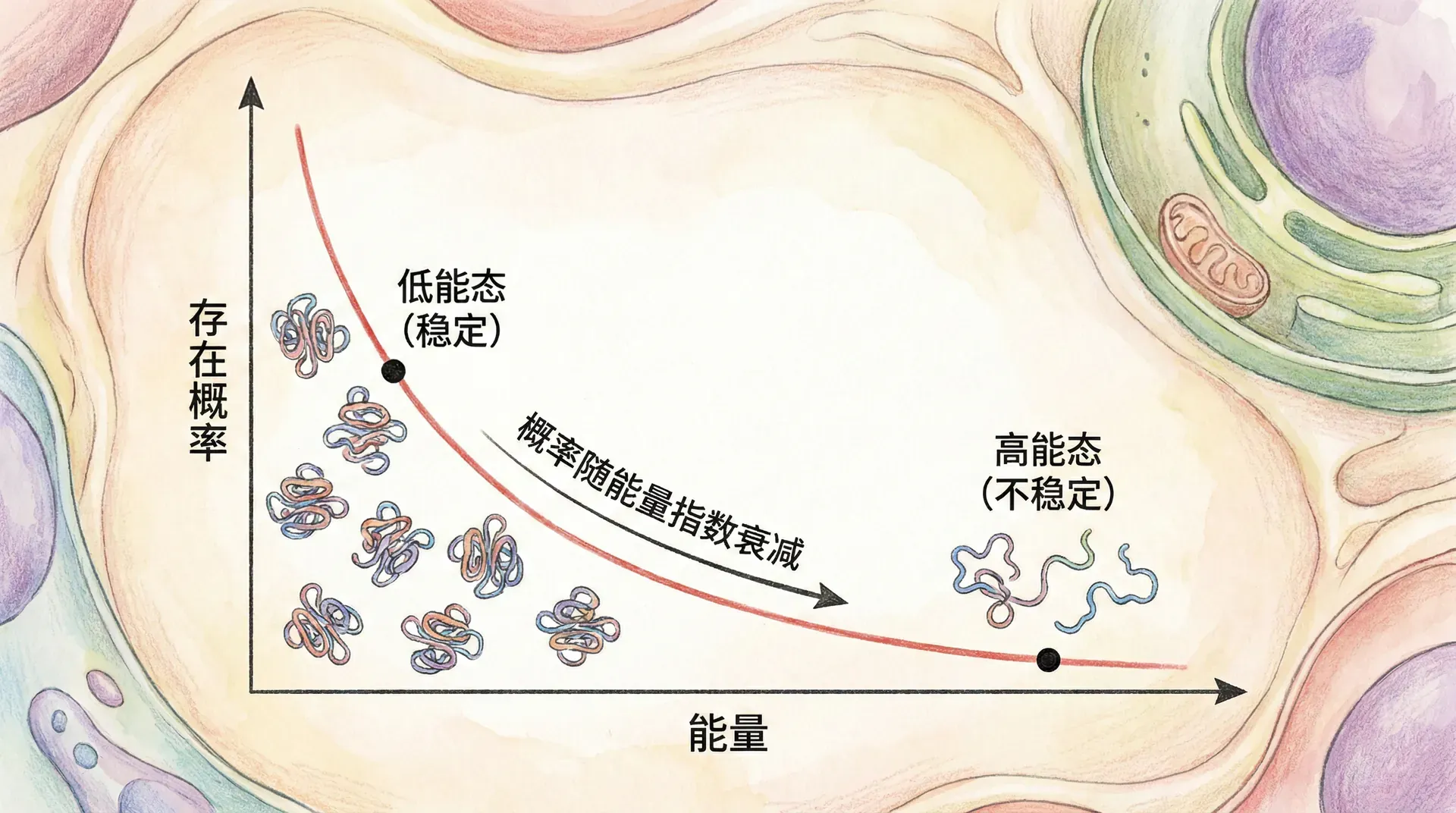
从上图我们可以看到,温度越低,大多数分子聚集在低能级,只有极少数能够“攀爬”到高能级;而在高温下,分子分布更为均匀,高能级的分子数量明显增加。这其实与我们在生活中的体验异曲同工:温暖情况下,人们更愿意分散在不同区域,而寒冷时则会本能地往温暖低处集中。这一分布规律是生命体适应环境、调节能量代谢的基础动力之一,也为下一步理解生命的复杂性打下了基础。
玻尔兹曼分布的指数形式
从经验到理论的飞跃
19世纪的奥地利物理学家路德维希·玻尔兹曼(Ludwig Boltzmann)通过对大量实验现象的分析和数学推导,提出了分子在不同能级上的分布应当遵循一个极为优美的指数关系。这个关系不仅通过理论得出,也在无数实验中被证实,如同中国古代数学家苦心积虑计算圆周率,最后发现其蕴藏着统一、恒定的规律一样,玻尔兹曼打开了一扇通往自然界深层数学秩序的窗户。
这一数学规律的经典表达式为:
其中,N(E) 表示能量为 E 的分子数目,N₀ 为归一化系数,k 是著名的玻尔兹曼常数,其数值约为 1.38 × 10⁻²³ J/K,T 是绝对温度(开尔文)。这一公式意味着:系统中能量越高的分子,其出现的概率就越低,且衰减速度呈现指数性。在温度升高的情况下,同一能级分子的数量分布会更“平展”,高能级分子的相对数量也会随之上升。
更直观的理解
为什么会是指数关系?假设楼梯越来越高,每高一级,往上攀爬所需的能量就要成倍增加。蹲在底层的人最轻松,愿意冲到顶层的“勇敢者”则越来越少。系统内的大多数分子宁可待在低能态,只有极少数能够“幸运地”获得更多能量跳到高能级。温度越高,相当于大家都变得更有力气,可以攀得更高,但整体还是遵循概率规律分布。
指数函数的生物学意义
这个指数分布不仅是物理教科书中的抽象概念,更深刻影响着生物世界的方方面面。例如:
- 酶催化反应的温度依赖性:生化反应速率常数遵循阿伦尼乌斯方程 ,其中 是活化能。这其实就是玻尔兹曼分布在反应动力学中的直接体现。只有分子达到或超过活化能阈值,反应才能发生;不同温度下,这样的分子数量比例就由玻尔兹曼分布决定。
- 信号分子通道的激活阈值:许多生物传感器(如离子通道)只有在膜电位涨到一定水平、“粒子”能量跨过阈值时才能被激活,这一概率同样符合扩展意义上的玻尔兹曼分布。
- 分布调控、适应性与进化:高能分子的活跃分布,使生物系统具备挑战突变、环境极端等条件时的多样准备和弹性。
日常体验的指数规律
比如感冒发烧时,为什么我们感到浑身无力?因为温度变化打乱了体内分子的能级分布,低能态与高能态的流转速率被重新分配,生理反应速度也随之改变。这种温度带来的“内在动力平衡”变化其实背后也有玻尔兹曼分布的影子。
茶叶冲泡中的玻尔兹曼分布
中国茶文化为玻尔兹曼分布在日常生活中的现象提供了极妙的例证。当我们用不同温度的水冲泡茶叶时,可以直接观察到活性成分的释出量随着温度陡增的“跳跃”现象:
随着水温升高,更多分子获得“跨越”出细胞壁和结构的能量门槛,能够在短时间内大量释放出来。这并不是线性关系而是随着温度的提高,关键分子的释放率近似指数增长。这背后对应的本质原因,就是高温时“足够能量”的分子增加速度是极快的。
换句话说,热水冲茶并非“机械地加快”了反应过程,而是彻底改变了分子的能量分布状态,让高能态分子成倍增长。中国古代烹茶讲究火候,实质上就是在调控分子的不同能级分布,以求最佳口感与营养释放。不仅茶叶,咖啡萃取、药材煎煮、甚至人体的热敷疗法,都因为玻尔兹曼分布而展现出温度调节下活性成分释放与吸收的“非线性”剧变。
上图展示了不同温度下玻尔兹曼分布的变化,可以直观地看到:温度越高(色彩越暖),高能级分子的比例明显升高,分布更为“平展”。这就是茶叶冲泡、酶反应活性、生态适应性等背后的关键物理机制。
配分函数与能级可及性
配分函数
配分函数(Partition Function, 通常记作 )是统计力学中的核心概念,我们可以把它比作生物系统的“身份证”或者“档案袋”——它记录了系统在当前条件下所有可能能量状态的“统计特征总和”。换言之,如果你了解了一个系统的配分函数,你就可以推导出它的绝大多数宏观物理性质(如能量、熵、自由能等)。
配分函数的数学表达式为:
其中 表示系统第 个可能的能级,求和遍历所有微观状态。
配分函数的物理意义
- 它衡量了整个系统“能级可及性的权重总和”。
- 某一具体能级 上分子的概率,即 ,这展示了配分函数的归一化作用。
生物分子的配分函数应用
配分函数在生物系统(例如蛋白质折叠、分子聚集等)中的应用非常广泛:
比如,生物体感冒发烧时,体温升高会影响分子构象的“选择概率”,一些异常折叠态(本来几乎不被占据)概率提高,这可能影响免疫应答和疾病过程。
中医经络理论的解读
如果用现代统计力学配分函数的语言重新审视传统中医的经络系统,可以将其类比为一个人体能量分布的“复杂网络”:每个经络、每个穴位都对应着生物分子的特定能级或状态。整个经络网络的配分函数决定了系统内部“气”的分布概率——某个穴位能量状态的提高或降低,都会影响全局能量的再分配。
基于这个模型,我们可以用新的科学视角理解诸如针灸等传统医学操作。通过局部施加刺激(如针灸某一穴位),可能会局部快速调节特定能级的分布、改变配分函数,进而波及整个能量分布,恢复系统平衡。尽管该解释还有待更多科学验证,但它为中西医学在能量调控层面的对话打开了新的思路。
值得一提的是,类似的配分函数思想在全球许多传统医学和养生理论中都能找到某种“影子”,这展现了人类对能量平衡与分布的高度关注。不论是养气调神、配伍食疗,还是现代分子药理,都可以从统计分布与系统配分的角度寻找共通点。
总之,玻尔兹曼分布和配分函数这两大概念不仅构成了统计物理和热力学的核心,也为我们理解生命现象、阐释跨文化的医学与日常经验提供了强有力的理论基础。
温度与熵的关系
温度
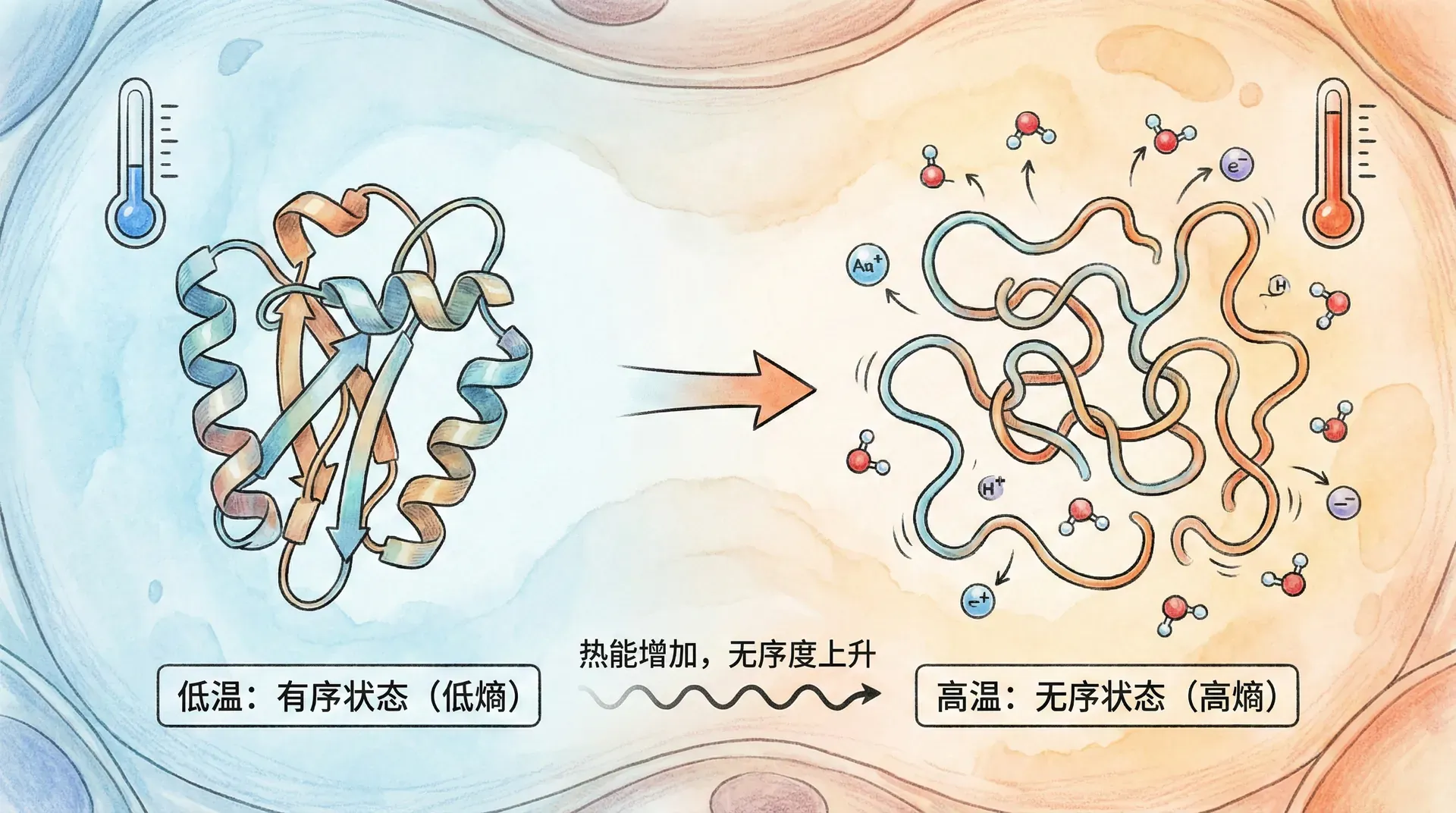
温度不仅仅是我们日常感受到的冷热程度,从统计热力学的角度来看,温度是分子平均动能的度量,是所有分子微观的无序运动(平动、转动、振动等)能量的宏观体现。而在更深层次的统计含义上,温度还能用来描述系统内能量分布的"宽度"或能级可及的“自由度”——温度越高,分子在不同能级间分布得越“分散”;温度越低,分子更倾向于集中在低能级。
在生物系统中,温度的变化会显著影响生物分子的行为。例如,人体体温维持在37°C左右,这个温度恰好使得大多数生物反应能够以适中的速率进行,既不会因温度过低而反应缓慢,也不会因温度过高而导致蛋白质变性和酶的失活。事实上,不同生物适应了不同的体温环境:北极动物通过调节体温适应寒冷环境,而嗜热菌则能在接近沸腾的热泉中繁衍生息,这些都体现了温度对生物系统分子活动乃至生态分布的深刻影响。
温度不仅影响分子的能量分布,也影响化学反应的方向和速率。生物体内的许多过程(如DNA双链解链、细胞膜相变、蛋白质结构转变等)都非常敏感于温度的微小变化。例如,细胞内的热休克蛋白会在体温升高时表达上调,以帮助受热变性的蛋白质重新折叠,维持细胞的生命活动。
熵与温度的互动关系
熵(Entropy)和温度之间存在着密不可分的深刻联系。熵是描述系统无序度和微观状态总数的物理量,定义为 ,其中 表示系统的多重度,而 是玻尔兹曼常数。从热力学第一和第二定律的结合出发,有著名的关系:。这个简单的微分关系揭示了熵增加的速率与温度成反比——在低温下,能量微小变化会导致更大的熵增(系统微观状态数剧烈增加);而在高温下,要想获得同样的熵变,则需要更大幅度的能量输入。
从统计力学角度说,温度高时,系统“容许”的微观状态较多(分子在高能级分布的概率显著增加),这使系统的熵值更高。反之,在极低温时,大部分分子只能停留在最低能态,系统的有序性增强,熵降低。这一原理也解释了为啥生物系统需要保持合适的温度区间来实现最优的生命活动:温度过低时,能量分布受限、熵增受阻,化学反应难以进行;温度过高时,虽然熵增加,但有序结构(如蛋白质)可能解体,导致功能丧失。
熵与温度的关系还体现在自由能表达式 (吉布斯自由能)中。随着温度的升高, 项加大,有利于那些有利于熵增加的过程进行(比如蛋白质折叠展开、化学反应的平衡转移等)。这也是为什么温度变化往往是生化过程调控的重要“开关”。
发酵过程中的温度控制
中国传统的发酵食品制作工艺为温度与熵关系的调控提供了丰富实践。例如制作豆豉、酱油、醪糟等食物时,温度的精确调控直接决定发酵微生物的种类和活性,为最终风味和质地的形成奠定基础。
以制作豆豉为例:
在整个发酵过程中,每一个阶段的温度控制都在无形中调节着系统的熵产速率——低温启动初期有利于种群萌发和分化,温度上升后菌丝和酶系迅速拓展,熵(无序度)急剧增长;最后随着温度减缓和风味物质的生成,系统熵达到相对平衡和稳定。这些精妙的温度调控,是千百年来经验积累的结晶,其科学本质正是温度与熵的动态平衡。
同样的温度调控原则在现代葡萄酒、酸奶、纳豆等发酵食品制造中也有极大应用,为人类带来丰富多彩的饮食文化。
上面展示了温度对不同酶类活性的影响。可以看到,人体消化酶的活性在体温附近(37°C)达到最高,超过这一温度酶活性急剧下降;而嗜热菌的酶却在60-70°C呈现峰值。微观层面,这些现象反映了酶结构的热稳定性和分子运动范围的变化,实质上也是温度影响下熵和能量分布的宏观体现。
热接触系统的能量交换
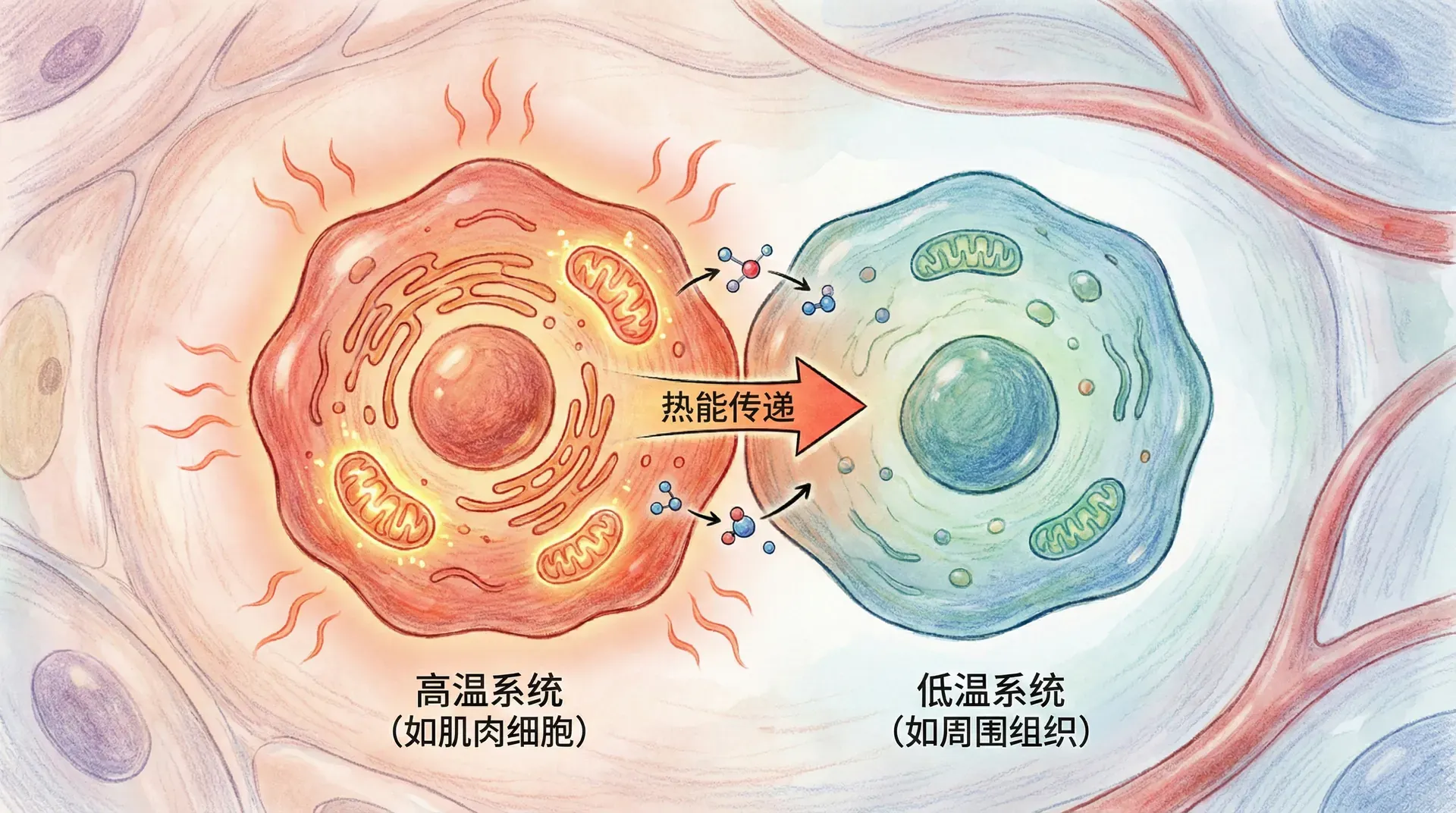
能量交换的平衡原理
当两个系统发生热接触时,能量会自发地从温度较高的系统传递到温度较低的系统,直到两者达到热平衡状态。这个过程本质上体现了系统熵的增加趋势(最大熵原理):能量分布越来越均匀,无序度(熵)不断升高,直到系统无法自发继续改变。
从分子角度看,热量的本质是大量微观粒子的无序运动和随机碰撞。热量从高温向低温传递,是因为高温系统中的分子动能更高,与低温系统混合后,总体的能量分布变得更“宽”,熵随之增大。
在生物学领域,这种能量交换机制广泛存在。例如,细胞内的ATP分子通过高能磷酸键水解,将化学能传递给其他分子,使各类生命活动(如运动、主动转运、酶合成等)得以顺利进行。这里的“高能系统”与“低能系统”之间的转化始终受熵增和热力学定律的约束。
此外,地球生态系统的能量流动,如太阳能通过光合作用进入生物圈,再被动物摄取和分解,整个过程正是能量从集中有序流向分散无序(熵增)的自然演化。
人体体温调节系统
人体的体温调节是热接触系统能量交换的一个经典实例。人体在不同环境温度下需要通过一系列生理调控机制来确保核心体温的恒定(约37°C),否则酶和细胞功能会受损。
具体调节机制包括:
- 皮肤血管舒缩:人在寒冷时,皮肤血管收缩减少散热;炎热时血管扩张加强散热。
- 汗腺分泌:通过出汗蒸发皮肤上的水分,吸收热量、帮助降温。
- 肌肉颤抖:在低温环境下(如冬季),肌肉颤抖增加产热,补偿体温流失。
- 激素调节:如甲状腺素、肾上腺素等代谢激素调控基础代谢率,间接影响产热和散热。
这些多系统协调的生理调节过程,每一个环节都符合热力学第二定律和最大熵原理,即通过能量重新分配和无序度提升使生命系统维持动态平衡。
体温调节涉及多个器官系统的协调工作,包括皮肤血管的舒缩、汗腺的分泌、肌肉的颤抖、代谢激素调节等,这些过程都遵循热力学第二定律和最大熵原理,保证了人体在环境变化中的稳态生存能力。
此外,体温调控“失灵”时会出现高热(如感染引起的发烧)或低体温症等情况,这实际上反映了生理调控未能实现应有的热能和熵的动态平衡,影响生命活动的正常进行。
中药炮制中的热力学原理
中药的炮制工艺(如炒制、蒸煮、烘焙等)是传统医学领域能量交换和热力学原理具体应用的典范。以炒制黄芩为例,通过精确控制加热温度、时间,使药材中复杂有机分子的构象发生改变,部分结合键断裂、部分新键形成,从而影响有效成分的活性与释放。这一过程中,热能自外部传入药材分子系统,推动分子重新排列,系统的微观状态数增多,熵显著增加。
中药炮制过程中常讲究“火候”——既要充分促使分子转化、有效成分充分显现,又要避免能量过量导致药材炭化或有效成分降解,这正是热能分布和熵变权衡的体现。现代药理学研究也证实,不同炮制温度和时间对中药有效组分含量和生物利用度会产生巨大影响,本质上仍然与热力学的能量分配规律密切相关。
总结
玻尔兹曼分布不仅是连接宏观热力学与微观分子运动的核心桥梁,也是解析生物系统能量分布和自发过程的重要理论基础。从分子的蛋白质折叠与酶活调控,到细胞能量流转,再到整个机体体温调节、生态能量转移、以及中药炮制等多层次的生物现象,其本质都可归结为能量、熵和温度三者的动态平衡与关联。
这些原理在发酵温度控制、蛋白自组装、生态系统能量流动与中药加工等实际案例中有着直接体现。理解熵与能量分布规律,有助于我们观察和分析更复杂的生物过程,例如跨膜物质转运、信号传递、基因表达调控等。后续我们也将进一步拓展到自由能、分子动力学与反应平衡领域,逐步揭示生命多样性及调控的物理根基。
如同老子所言:“道生一,一生二,二生三,三生万物。” 简单的能量分布法则孕育出丰富多彩的生命现象,正是熵增规律与玻尔兹曼分布共同推动了生物世界由简单走向复杂的壮丽演化。