大O表示法
在编程的世界里，我们经常面临一个灵魂拷问：当用户从10个变成1000万个时，你的代码还能跑得动吗？
假设你正在整理一个图书馆：
- 如果只有10本书，你闭着眼睛乱放都能很快找到。
- 但如果有100万本书，如果没有一套科学的索引系统，找一本书可能要花上一辈子。
这就引入了我们今天的主角——大O表示法。
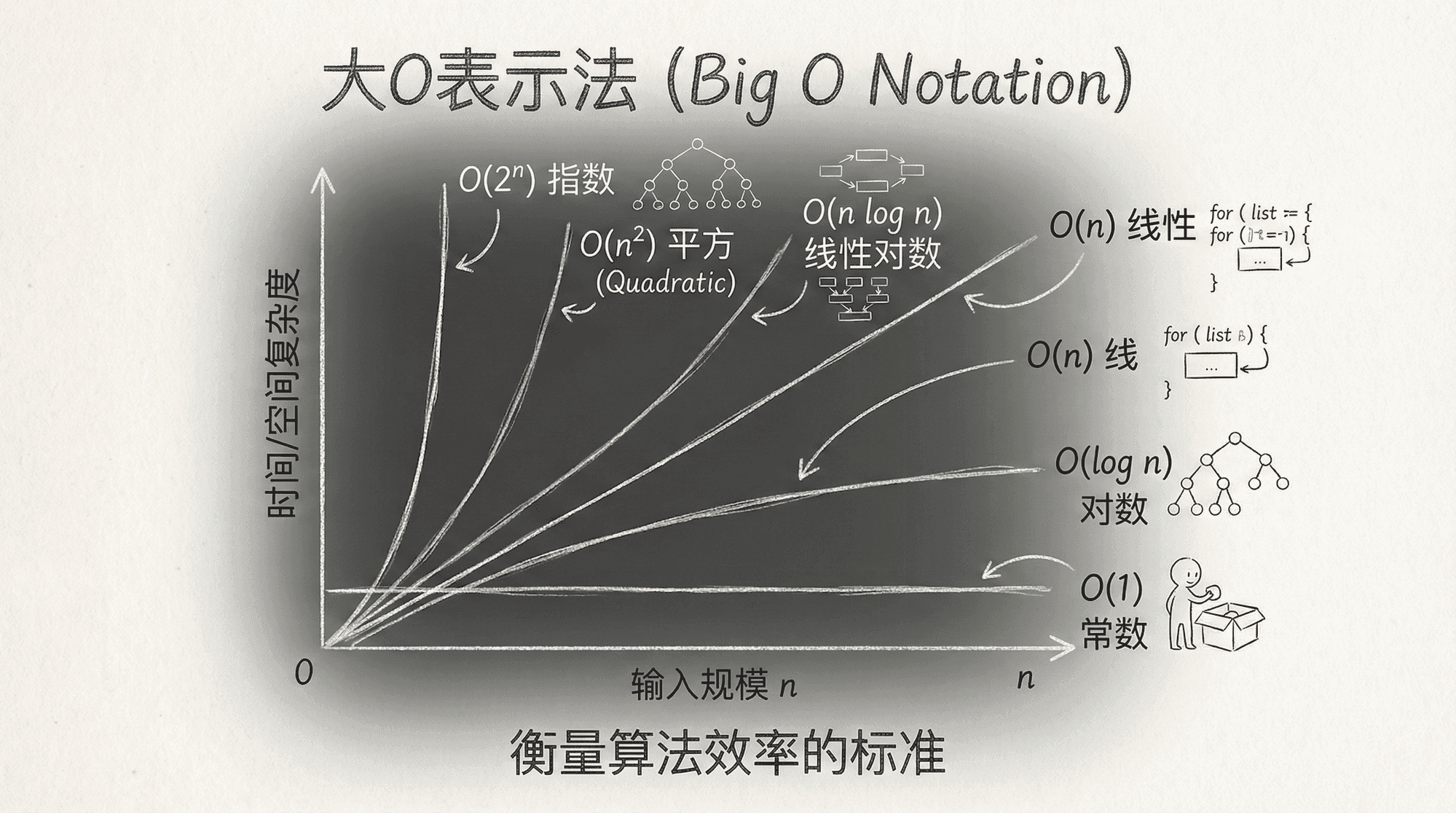
到底什么是大O表示法？
简单来说，大O表示法（Big O Notation） 是程序员用来吐槽代码“效率”的一种通用语言。它不计算具体的秒数（因为不同的电脑运行速度不同），它计算的是趋势。
随着输入数据量（n）的增加，程序的运行时间或占用内存会变慢/变大多少？
常见的时间复杂度（由快到慢）
为了方便理解，我们将常见的几种复杂度按“效率”从高到低排列：
O(1) - 常数时间 (最快)
含义： 不管数据有多少，耗时都一样。这是最理想的状态！
举例： 假设你知道朋友家的具体门牌号。无论这个城市有10个人还是1000万人，你都能直接导航到他家门口，不需要挨家挨户找。
|#include <vector> using namespace std; int getFirstElement(const vector<int>& arr) { // 就像你有任意门的钥匙，直接到达目的地 return arr[0]; } // 无论数组里有10个数据还是10亿个，这一步操作瞬间完成。 // 这就是O(1)的特征：时间不随输入规模变化
O(log n) - 对数时间 (非常快)
含义： 数据量翻倍，时间只增加一点点。通常出现在“二分查找”中。
举例： 猜数字游戏（1-100）。 你问：“是50吗？” 对方：“低了”。 你瞬间排除了1-50这一半的数字！每次都能排除一半的可能性，这效率极高。
|#include <vector> using namespace std; // 二分查找：经典的 O(log n) int binarySearch(const vector<int>& sortedArr, int target) { int left = 0; int right = sortedArr.size() - 1; while (left <= right) {
O(n) - 线性时间 (普通)
含义： 数据量增加几倍，耗时就增加几倍。中规中矩。
举例： 看书。书越厚，看完需要的时间就越长。如果你要在一本没目录的书里找一句话，最坏的情况必须从第一页翻到最后一页。
|#include <vector> using namespace std; int findElement(const vector<int>& arr, int target) { // 必须老老实实从头走到尾 for (int i = 0; i < arr.size(); i++) { if (arr[i] == target) { return i;
O(n²) - 平方时间 (有点慢)
含义： 数据量增加，耗时呈指数级爆炸增长。通常涉及“双层循环”。
举例： 班级聚会握手。 班里有n个同学，每个人都要和其余n-1个同学握手。 如果是10人，握手次数还好；如果是1000人，握手次数就是百万级的！
|#include <vector> using namespace std; // 冒泡排序：典型的 O(n²) void bubbleSort(vector<int>& arr) { int n = arr.size(); for (int i = 0; i < n - 1; i++) { // 外层：每个人都要轮一遍 for (
为什么这东西很重要？
假设你日后要做一个“商品搜索”功能，超市有100万件商品。
方案 A：暴力搜索 (O(n))
- 做法： 每次用户搜“苹果”，你都派人去仓库把100万件商品标签看一遍。
- 结果： 用户搜一次要等3秒。如果有1万个人同时搜，服务器直接爆炸。
方案 B：索引搜索 (O(1) ~ O(log n))
- 做法： 开业前先辛苦一点，建立一个“索引本”（比如 'P' 这一页专门记苹果在哪里）。
- 结果： 用户搜“苹果”，直接翻索引本，0.001秒出结果。
结论： 好的算法（低时间复杂度）能帮你省下巨额的服务器费用，还能让用户觉得你的软件“真快”！
可视化时间复杂度
空间复杂度：不仅要快，还要省
除了关心“快不快”（时间），我们还得关心“占地大不大”（内存）。这就是 空间复杂度。
举例：搬家
- 空间 O(1)： 原地整理。你不需要额外的箱子，直接在屋子里挪动家具。（省空间，比如冒泡排序）
- 空间 O(n)： 复制一份。为了整理书架，你把书全部搬到另一个空房间里重新排。（费空间，比如归并排序）
示例对比：
|// 🟢 省空间：选择排序 // 只用了一个临时变量 temp，无论数组多大，额外空间都是固定的 O(1) void selectionSort(vector<int>& arr) { // ... 直接在原数组 arr 上修改 ... } // 🔴 费空间：归并排序 // 需要创建新的 vector (left, right) 来暂存数据 // 数据越多，需要的额外内存越大 -> O(n) vector<int> mergeSort(const vector<int>& arr) { vector<int> left = ...; // 申请新内存 vector
在现在的计算机设备上，内存通常比较充足，所以有时候为了追求极致的速度（时间），我们会愿意牺牲一些内存（空间）。这就是传说中的**“空间换时间”**。
小练习
- 一个函数遍历数组一次，对每个元素执行常数时间操作，时间复杂度是？
- 一个循环，循环变量每次乘以2，直到达到n，时间复杂度是？
- 递归版本的斐波那契数列（无记忆化）的时间复杂度是？
4. 分析函数的时间复杂度练习
分析以下函数的时间复杂度：
- 函数A：
sumArray函数遍历数组一次，计算所有元素的和 - 函数B：
mysteryFunction函数中，循环变量每次乘以2（1, 2, 4, 8...） - 要求：分析每个函数的时间复杂度，并说明原因
- 提示：函数A像把书从头翻到尾，函数B像切蛋糕每次切一半
|#include <iostream> #include <vector> using namespace std; // 函数A：计算数组和 int sumArray(const vector<int>& arr) { int sum = 0; for (int i = 0; i < arr.size(); i++) // 循环 n 次
5. 斐波那契数列的陷阱练习
实现斐波那契数列的两个版本，对比它们的性能差异：
- 版本1（递归）：使用递归实现，无记忆化
- 版本2（动态规划）：使用循环和数组记录已计算的值
- 要求：实现两个版本，并分析它们的时间复杂度
- 测试：计算
fibonacci(10)和fibonacci(40)，观察性能差异
|#include <iostream> #include <vector> #include <chrono> using namespace std; using namespace std::chrono; // 版本1：递归版本（无记忆化）- 时间复杂度 O(2ⁿ) long long fibonacciRecursive(int n) { if (n <= 1) return n; // 问题：会重复计算大量子问题 // 例如：fib(5) = fib(4) + fib(3) // fib(4) = fib(3) + fib(2) // fib(3) = fib(2) + fib(1)